Problem 1
We have $10,000$ identical equilateral triangles. Consider the largest regular hexagon that can be formed with these triangles without overlapping. How many triangles will not be used?
Solution
Answer: $400$.
Let $n$ be the length of the side of the largest regular hexagon. Notice that the hexagon consists of $6$ equilateral triangles, each formed by $n^2$ smaller equilateral triangles. Therefore we have an inequality
$$ 6n^2 < 10,000 < 6(n+1)^2 $$
which implies that $39<n<41$ and therefore $n=40$. The number of unused triangles is therefore equal
$$ 10,000 – 6 (40)^2 = 400 $$
Problem 2
The cost of $1000$ grams of chocolate is $x$ dollars and the cost of $1000$ grams of potatoes is $y$ dollars, the numbers $x$ and $y$ are positive integers and have not more than $2$ digits. Mother said to Maria to buy $200$ grams of chocolate and $1000$ grams of potatoes that cost exactly $N$ dollars. Maria got confused and bought $1000$ grams of chocolate and $200$ grams of potatoes that cost exactly $M$ dollars ($M>N$). It turned out that the numbers $M$ and $N$ have no more than two digits and are formed of the same digits but in a different order. Find $x$ and $y$.
Train for Math Olympiads
Learn moreSolution
Answer: $x=50$, $y=5$.
Let $N=\overline{ab}=10a+b$ and $M=\overline{ba}=10b+a$, where $a<b$ are some digits. Let us write the system of equations
$$ \frac{x}{5} + y = 10a+b $$
$$ \frac{y}{5} + x = 10b+a $$
By adding these equations we have
$$ \frac{6}{5} \cdot (x+y) = 11(a+b) $$
$$ 6 (x+y) = 55(a+b) $$
By adding these equations we have
$$ \frac{4}{5} \cdot (x-y) = 9(b-a) $$
$$ 4 (y-x) = 45(a-b) $$
This implies that $a+b$ is a multiple of $6$ and $b-a$ is a multiple of $4$. Since $0<a+b \leq 9 + 9 = 18$, then the only multiples of $6$ that should be considered are $6$, $12$, $18$.
$Case$ $1$: $a+b=6$. If $b-a=0$, then $a=3$, $b=3$, contradiction with $a<b$. If $b-a=4$, then $b=5$, $a=1$ and the costs of chocolate and potatoes are $x=50$, $y=5$.
$Case$ $2$: $a+b=12$. If $b-a=0$, then $a=6$, $b=6$ contradiction with $a<b$. If $b-a=4$, then $b=8$, $a=4$ and the costs of chocolate and potatoes $x=\frac{155}{2}$, $y=\frac{65}{2}$ are not integers. If $b-a=8$, then $a=10$, $b=2$ and $a$ is not a digit.
$Case$ $3$: $a+b=18$. Since $a+b \leq 9 + 9 = 18$, then $a=9$, $b=9$ contradiction with $a<b$.
Problem 3
The side $BC$ of the triangle $ABC$ is extended beyond $C$ to $D$, such that $CD=BC$. The side $CA$ is extended beyond $A$ to $E$, such that $AE=2CA$. Prove that if $AD=BE$, then the triangle $ABC$ is right.
Solution
Let us extend the side $AC$ is extended beyond $C$ to $F$, such that $CF=CA$. Since $BC=CD$, then $ABFD$ is a parallelogram and $BF=AD$. Therefore the triangle $EBF$ is isosceles. Since $AE = 2 CA = CA+CF = AF$, then $BA$ is the median of the triangle $EBF$. Therefore it is also its height and $\angle BAC = 90^{\circ}$.
Problem 4
Determine all integers $m$, for which it is possible to dissect the square $m \times m$ into five rectangles, with the side lengths being the integers $1$, $2$, … , $10$ in some order.
Solution
Answer: $m=11$, $m=13$.
Let the dimensions of the five rectangles be $a_1 \times b_1$, $a_2 \times b_2$, $a_3 \times b_3$, $a_4 \times b_4$ and $a_5 \times b_5$. By AM-GM inequality we have
$$ a_1b_1 + a_2b_2 + a_3b_3 + a_4b_4 + a_5b_5 \geq 5 \sqrt[5]{a_1b_1a_2b_2a_3b_3a_4b_4a_5b_5} = 5 \sqrt[5]{10!} >102 $$
which implies that the total area of the rectangles is greater than $100$ and therefore $m \geq 11$.
From the inequality
$a_ib_i \leq \frac{a_i^2+b_i^2}{2}$
we have
$$ a_1b_1 + a_2b_2 + a_3b_3 + a_4b_4 + a_5b_5 \leq \frac{a_1^2+b_1^2+a_2^2+b_2^2+a_3^2+b_3^2+a_4^2+b_4^2+a_5^2+b_5^2}{2} = $$
$$ \frac{1^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2+9^2+10^2}{2} =192.5 $$
which implies that the total area of the rectangles is less than $196$ and therefore $m \leq 13$.
Let us show that $m=12$ does not work. Let us assume that it is possible to cover the square $12 \times 12$ with five rectangles of side lengths being the integers $1$, $2$, … , $9$, $10$ in some order. Since each rectangle can cover at most one corner of the square $12 \times 12$, then the four corners are covered by different rectangles. If there is a space between some of these $4$ rectangles, then it cannot be covered by the fifth rectangle. Therefore the covering should be as the one below.
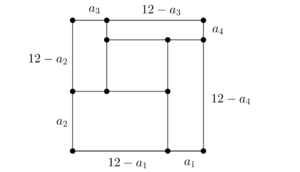
Note that the sides are divided into pairs that complement to $12$. The only sides that do not have a side that complements them to $12$ are $1$ and $6$. Therefore the interior rectangle is $1 \times 6$ and without loss of generality we have
$$ 12 -a_1-a_3=6 $$
$$ 12 -a_2-a_4=1 $$
which implies that $a_1+a_3=6$ and $a_2+a_4=11$.
Without loss of generality we can assume $a_1<a_3$. From the first equality $1 \leq a_1 \leq 3$, which gives the following pairs for $(a_1,a_3)$: $(1,5)$, $(2,4)$, $(3,3)$. Notice that $(3,3)$ uses the same side twice and the side $1$ is already used in the interior rectangle. Therefore we have $a_1=2$ and $a_3=4$.
Without loss of generality we can assume $a_2<a_4$. From the first equality $1 \leq a_2 \leq 5$, which gives the following pairs for $(a_2,a_4)$: $(1,10)$, $(2,9)$, $(3,8)$, $(4,7)$ and $(5,6)$. Notice that the sides $1$, $2$, $4$ and $6$ has already been used. Therefore we have $a_2=3$ and $a_4=8$. However the side $8$ has already been used as $12-a_3=8$. Contradiction.
It is not hard to see that the rectangles $3 \times 6$, $4 \times 7$, $2 \times 8$, $1 \times 9$, $5 \times 10$ will form a square of side $m=11$ and the rectangles $1 \times 2$, $3 \times 7$, $4 \times 6$, $5 \times 10$, $8 \times 9$ will form a square of side $m=13$.



