Problem 4
How many numbers $\overline{abcd}$ with different digits satisfy the following property: if we replace the largest digit with the digit $1$ results in a multiple of $30$?
Solution
Answer: $162$
Let us call the numbers satisfying the conditions of the problem $boring$. Let us find the total number of boring numbers. Notice that $30=2 \cdot 3 \cdot 5$. Since $30 | \overline{abcd}$, then $d=0$. Let one of the digits $a$, $b$ or $c$ has been replaced by $1$. The sum of these three digits therefore should be a multiple of $3$, while one of the remaining digits is $1$. Since $0<1+x+y \leq 1+9+9 <21$ for the digits $x$ and $y$, then we can do the casework on the sum of the digits, which can only take values following: $3$, $6$, $9$, $12$, $15$ and $18$.
Sum of digits is $3$. The possible numbers are $102$, $120$, $201$, $210$, where $1$ was replaced by one of the digits $3$, $4$, $5$, $6$, $7$, $8$ or $9$. This gives a total of $4 \cdot 7 = 28$ boring numbers.
Sum of digits is $6$. The possible numbers are $124$, $142$, $214$, $241$, $412$, $421$, where $1$ was replaced by one of the digits $5$, $6$, $7$, $8$ or $9$ and also the numbers $105$, $150$, $501$, $510$, where $1$ was replaced by one of the digits $6$, $7$, $8$ or $9$. This gives a total of $6 \cdot 5 + 4 \cdot 4 = 46$ boring numbers.
Sum of digits is $9$. The possible numbers are $108$, $180$, $801$, $810$, where $1$ was replaced by the digit $9$, the numbers $126$, $162$, $216$, $261$, $612$, $621$, where $1$ was replaced by one of the digits $7$, $8$ or $9$, and also the numbers $135$, $153$, $315$, $315$, $513$, $531$, where $1$ was replaced by one of the digits $6$, $7$, $8$ or $9$. This gives a total of $4 \cdot 1 + 6 \cdot 3 + 6 \cdot 4 = 46$ boring numbers.
Sum of digits is $12$. The possible numbers are $138$, $183$, $318$, $381$, $813$, $831$, where $1$ was replaced by the digit $9$, the numbers $147$, $174$, $417$, $471$, $714$, $741$, where $1$ was replaced by one of the digits $8$ or $9$, and also the numbers $156$, $165$, $516$, $561$, $615$, $651$, where $1$ was replaced by one of the digits $7$, $8$ or $9$. This gives a total of $6 \cdot 1 + 6 \cdot 2 + 6 \cdot 3 = 36$ boring numbers.
Sum of digits is $15$. The possible numbers are $168$, $186$, $618$, $681$, $816$, $861$, where $1$ was replaced by the digit $9$. This gives a total of $6 \cdot 1 = 6$ boring numbers.
AMC 8 Preparation Book
Order Now
Therefore the total amount of boring numbers is
$$ 28+46+46+36+6 = 162 $$
Problem 5
Circle $r$ contains the circles $m$, $p$ and $r$, such that they are tangent to $r$ internally and any two of them are tangent between themselves. The radii of the circles $m$ and $p$ are equal $x$. The circle $o$ has radius $1$ and passes through the center of the circle $r$. Find the value of $x$?
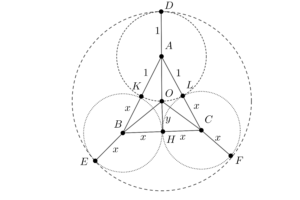
Solution
Answer: $\frac{8}{9}$.
Let $OH=y$. From the Pythagorean Theorem for the triangle $BOH$ we have:
$$ BO^2 = BH^2 + OH^2 $$
or equivalently
$$ (2-x)^2 = x^2 + y^2 $$
$$ x^2-4x+4 = x^2 + y^2 $$
$$ -4x+4 = y^2 $$
From here we have
$$ y = 2 \sqrt{1-x} $$
From the Pythagorean Theorem for the triangle $BAH$ we have:
$$ BO^2 = BH^2 + OH^2 $$
or equivalently
$$ (x+1)^2 = x^2 + (y+1)^2 $$
$$ x^2+2x+1 = x^2 + y^2+2y+1 $$
$$ 2x = y^2+2y$$
Substituting $y = 2 \sqrt{1-x}$ we have
$$ 2x =-4x + 4 +4 \sqrt{1-x} $$
$$ 6x – 4 = 4 \sqrt{1-x} $$
$$ 3x – 2 = 2 \sqrt{1-x} $$
$$ 9x^2 – 12x + 4 = 4-4x $$
$$ 9x^2 – 8x = 0 $$
From here we have
$$ x = \frac{8}{9} $$
Problem 6
Two positive integers $n, m \geq 2$ are called allied if when written as a product of primes (not necessarily different): $ n = p_1p_2 … p_s$ and $m = q_1q_2 … q_t$, turns out that:
$$ p_1 + p_2 + … + p_s = q_1 + q_2 + … + q_t $$
(a) Show that the biggest ally of any positive integer has to have only $2$ and $3$ in its prime factorization.
(b) Find the biggest number which is allied of $2021$.
Solution
Answer: $3^{30}$.
For the part (a) let us assume the contrary, i.e. that the biggest ally $M$ of some positive integer $m$ has some other prime $p$ in its factorization other than $2$ and $3$. Obviously $p \geq 5$. Notice that any positive integer $x \geq 2$ can be represented as a sum of several $2$s and $3$s. Indeed if $x$ is even, then we just add $\frac{x}{2}$ primes $2$ and if $x$ is odd, then we just add one prime $3$ and $\frac{x-3}{2}$ primes $2$.
Now let $p=2a+3b$ for some positive integers $a$ and $b$. Let us show that the new number $M^{\ast}$ formed by the substitution of the prime $p$ by $a$ factors of $2$ and $b$ factors of $3$ is going to be greater than $M$. Indeed, it is sufficient to show that
$$ 2^a \cdot 3^b > p $$
By Bernoulli’s Inequality
$$ 2^a \cdot 3^b = (1+1)^a \cdot (1+2)^b \geq (1+a)(1+2b)$$
Notice that
$$ (1+a)(1+2b) = 1+2b+a+2ab > 1+2b+a+ab $$
However
$$ 1+2b+a+ab \geq 2a+3b $$
is equivalent to
$$ (a-1)(b-1) \geq 0 $$
which is true for positive integers $a$ and $b$.
Therefore
$$ 2^a \cdot 3^b > 2a+3b = p $$
For the part (b) notice that $2021 = 43 \cdot 47$, where $43$ and $47$ are primes and since $43+47=90$. By the part (a) the biggest allied number of $2021$ consists of $a$ primes $2$ and $b$ primes $3$. We also have
$$ 2a+3b=90 $$
First, notice that $a$ is divisible by $3$. Also, since $2+2+2=3+3$, then let us consider an operation of substituting three primes $2$ for two primes $3$. Since
$$ 2^3 < 3^2 $$
the product will become larger. Therefore for $a \geq 3$, we can obtain a larger allied number by applying this operation. This means that $a=0$ and the largest ally is $3^{30}$.



