Let us call a natural number interesting if any of its two consecutive digits form a number that is either a multiple of $19$ or $21$. How many interesting $2022$-digit numbers exist?
Solution
Answer: there are $9$ interesting $2022$-digit numbers.
Let $A$ be the set of all two-digit multiples of $19$ and $21$:
$$ A = \{19, 21, 38, 42, 57, 63, 76, 84, 95 \} $$
Notice each of the digits $1$ through $9$ appears exactly once as the first digit of some number in $A$ and exactly once as the second digit of some number in $A$. Furthermore, under the conditions of the problem the digits form a cycle:
$$ 1-9-5-7-6-3-8-4-2-1 $$
This means that the first digit of any $2022$-digit interesting number uniquely defines it. Since there are $9$ different possibilities for the first digit, then there is a total of $9$ such numbers.
Problem 2
There are sticks of length $1$ with number $1$, $2$, or $3$ written on each of them. There is an unlimited supply of sticks with every number. Two triangles are considered different if neither can be built with the stick of the other triangle.
(a) How many different triangles consisting of $3$ sticks are possible?
(b) Find the largest possible sum of the numbers written on the $9$ sticks on the boundary of the big triangle if all small triangles are different?
Solution
(a) It is not hard to see that there are only $10$ different triangles: $(1,1,1)$, $(1,1,2)$, $(1,1,3)$, $(2,2,2)$, $(2,2,1)$, $(2,2,3)$, $(3,3,3)$, $(3,3,1)$, $(3,3,2)$, $(1,2,3)$.
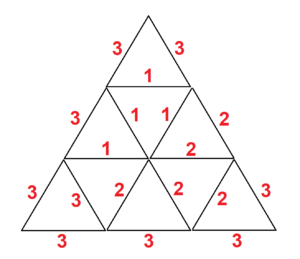
(b) Answer: $26$.
First, let us show that the largest sum cannot be $27$. Notice that there are only $6$ different triangles that contain the side $3$: $(1,1,3)$, $(2,2,3)$, $(3,3,3)$, $(3,3,1)$, $(3,3,2)$, $(1,2,3)$. If the sum is $27$, then all the boundary sticks have number $3$ on them, including the corner triangles. This implies that one of the corner triangles is $(3,3,3)$. This implies that there will be $7$ different triangles that contain the side $3$. Contradiction.
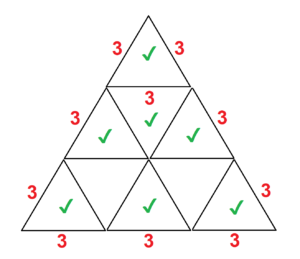
An example for the largest sum being $26$ is given below.
Problem 3
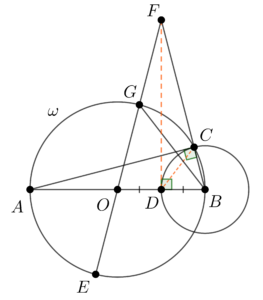
Let $\omega$ be a circle with center $O$ and diameter $AB$. A circle with center $B$ intersects $\omega$ at $C$ and $AB$ at $D$. The line $CD$ intersects $\omega$ at the point $E$ ($E \neq C$). The intersection of the lines $OE$ and $BC$ is $F$.
(a) Prove that the triangle $OBF$ is isosceles.
(b) If $D$ is the midpoint of $OB$, find the ratio $FB:BD$.
Solution
(a) Let $\angle DCB = y$. Since the triangle $CDB$ is isosceles, then $\angle CDB = y$ and $\angle CBD = 180^ {\circ} – 2y$. Let $G$ be the intersection of $OF$ with $\omega$ ($G \neq E$). Since $EGCB$ is cyclic, then $\angle EGB = \angle ECB = y$. Since the triangle $OGB$ is isosceles, then $\angle GBO = y$ and $\angle GOB = 180^ {\circ} – 2y$. From here $\angle CBD = \angle GBO$ and the triangle $OBF$ is isosceles.
(b) Answer: $4$.
Notice that since $D$ is the midpoint of $OB$, then $AB=4 \cdot BD$. Since $OBF$ is isosceles, then $FD$ is the median, and the altitude in the triangle $OBF$. From here the triangles $FDB$ and $BCA$ are similar and
$$ \frac{FB}{BD} = \frac{AB}{BC} = \frac{AB}{BD} = 4 $$
Problem 4
Let’s build a family $\{ K_n \}$ of geometric figures following the pattern, shown in the images, where each hexagon is built by cutting the two top corners of a square, such that the two figures removed are two identical isosceles triangles, and the three resulting top sides have the same length. Let $P_n$ and $A_n$ be the perimeter and the area of the figure $K_n$. The side of the square to construct $K_0$ is $x$.
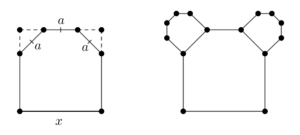
(a) Find $P_0$ and $A_0$ in terms of $x$.
(b) Find the explicit formulas for $P_n$ and $A_n$ in terms of $x$ and $n$.
Solution
(a) Answer: $P(0)=2\sqrt{2}x$, $A_0= \left( \frac{2\sqrt{2}-1}{2} \right) x^2$.
Let us call $a$ the length of the three equal segments. Then
$$ \frac{a}{\sqrt{2}} + \frac{a}{\sqrt{2}} + a = x $$
which implies that $a=\left( \sqrt{2}-1 \right)x$. From here
$$ P_0 = 4x – 4 \left( \frac{a}{\sqrt{2}} \right) = 2\sqrt{2}x $$
and
$$ A_0 = x^2 – \left( \frac{a}{\sqrt{2}} \right)^2 = \left( \frac{2\sqrt{2}-1}{2} \right) x^2 $$
(b) Let us put $k = \left( \sqrt{2}-1 \right)$, $\alpha = 2\sqrt{2}$, $\beta = \left( \frac{2\sqrt{2}-1}{2} \right)$.
Let us define $f(t)$ as the perimeter of the mentioned hexagon of the side $t$. Then from the part (a) we have that $f(t)=\alpha t$. Furthermore, we have
$$ P_0 = f(x) = \alpha x $$
$$ P_1 = f(x) + 2 \cdot \left( f(kx) – kx \right) = \left( \alpha-1 \right) x \left( 1 + 2k \right) +x $$
$$ P_2 = f(x) + 2 \cdot \left( f(kx) – kx \right) + 2^2 \cdot \left( f(k^2x) – k^2x \right) = \left( \alpha-1 \right) x \left( 1 + 2k +2^2k^2 \right) + x $$
Applying the formula for the sum of the geometric sequence we have
$$ P_n =\left( \alpha-1 \right) x \left( \frac{\left(2k\right)^{n+1}-1}{2k-1} \right) + x $$
Let us define $g(t)$ as the area of the mentioned hexagon of the side $t$. Then from the part (a) we have that $g(t)=\beta t^2$. Furthermore, we have
$$ A_0 = g(x) = \beta x^2 $$
$$ A_1 = g(x) + 2 \cdot g(kx) = \beta x^2 \left( 1 + 2k^2 \right) $$
$$ A_2 = g(x) + 2 \cdot g(kx) + 2^2 \cdot g(k^2x) = \beta x^2 \left( 1 + 2k^2 + 2^2k^4 \right) $$
Applying the formula for the sum of the geometric sequence we have
$$ A_n = \beta x^2 \left( \frac{\left(2k^2\right)^{n+1}-1}{2k^2-1} \right) $$



